Войти
Регистрация
1
Дробные числа
Опубликовал: Радуга:),
05 Февраль 2018
·
7 117 Просмотров
школа арифметика жизнь математика
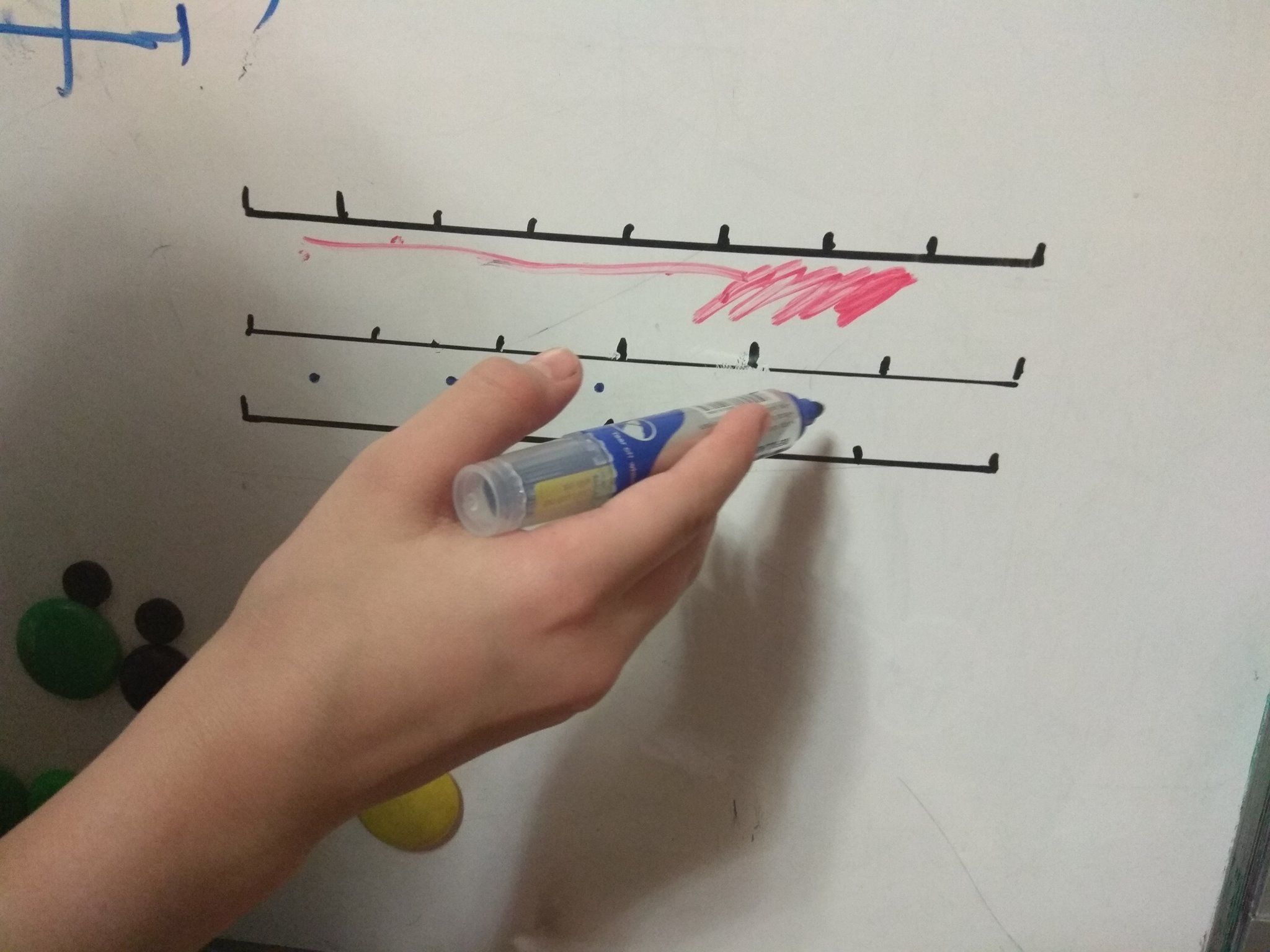- именно так называются они, а не просто "дроби".Это открытие - самая мелочь по сравнению с другими, которые сделали мы сегодня: я - при помощи "Методики Арифметики" Березанской, а Милана - при помощи доски, маркеров, бумаги, линейки и карандаша...)))
Конечно, гуманитарный мозг - хороший повод откосить от математики, но в нашей семье папа ни разу не педагог, хотя он и дом построить может, и трактор водить умеет, и машину разобрать-собрать, и чертежи трансформаторов читает быстрее, чем художественную литературу, и людьми руководит успешно.
Поэтому беру в руки толстенную Березанскую и ваяю рисунки на доске. Как в том анекдоте: "Пока объяснила - сама поняла"
Началось с того, что нужно было 3 отрезка поделить на 4 равные части несколькими способами. Не так просто, как кажется, Милана, глядя на отрезки, которые я старательно вывела перед занятием, долго возмущалась, почему при сложении трех кусочков, равных 1/4, будет 3/4?!
Всё время приговаривала "одна вторая", как мантру, и боролась со мной за правоту.
Я помню, в школе мы это решали механически: ну сложи 3 дроби, трудно, что ли?
А принцип? ведь за числами стоит суть. И мы начали её исследовать, когда сопротивление спало. Обычно это происходит на "второе китайское предупреждение". Потому что после третьего занятие заканчивается и все идут заниматься своими делами, во избежание конфликта
Милану злит, что нужно включать мозг.
- Это как хочешь. Хочешь знать дроби вхолостую, на уровне цифр, - дело твоё. Хочешь понять принцип - давай заниматься.
- Но одна вторая...
Я закатываю глаза и мы продолжаем.
- отрезаю 4 полоски бумаги и складываю каждый, чтобы получилось 4 куска. Целый лежит в стороне, от трёх Милана отрывает четверти.
Четверти складываются рядом и сравниваются с уцелевшим: вот откуда взялись 3/4. Дробь меньше единицы. Прожито.
Дальше кладём рядом 3/4 и 3/4 = 6/4. Как выглядит полоска в сравнении с уцелевшей? Вот что такое неправильная дробь - всегда больше единицы. Бинго.
- сложная задача - продолжаем делить 3 отрезка на 4 равные части. Самое простое - каждую поделить на четвертинки и раздать по три кусочка.
Дело пошло. Рисуется яблоко, делится на половины... еще немного- второе тоже на половины... и наконец третье делится на 4 части. Ура!
- третий способ предложил муж (который не смог допереть до второго) - сложить 3 отрезка вместе и поделить на равные части.
Я предложила только один, самый простой, первый
- сравнить дроби 7/8, 5/6 и 3/4.
Рисуем 3 отрезка по 24 см, делим, измеряем, ищем решение.
"Врагу не сдаётся наш гордый варяг" - Милана продолжает борьбу и в упор не видит различия между отрезками.
Получает задание начертить то же самое в тетради, самостоятельно, максимально точно. И после этого снова делает открытие:
дробное число - это какая-то часть от целого.
числитель указывает на количество кусочков
знаменатель - на сколько был разделён целый.
Конечно, они это всё уже неделю обсуждают на уроках математики. А проживается только сейчас: лучше 1 раз увидеть, чем 100 раз услышать, это про сенсориков)))
Проверка - приведение к общему знаменателю - пока мимо понимания. Рано. Это будет позже, после обкатки дробей в примерах.
- сравнить дроби 6/5, 5/4, 4/3, какая из этих дробей больше? на какую долю каждая из этих дробей больше единицы?
- сравнить 3/8 и 5/8 с половиной на рисунке и посмотреть, какая из них больше
- сравнить смешанные числа (представленные целым и дробным числом) - это была головоломка.
1. какую долю нужно добавить до целого числа?
2. сравнить доли между собой образно, без приведения к общему знаменателю. В очередной раз отметить, что 1/6 меньше, чем 1/5.
3. сделать вывод: чем меньшей дроби не хватает до целого, тем больше смешанное число
- округлить смешанные числа, добавляя недостающие дроби. Назвать ближайшие целые.
всё это они прошли в школе. Правда, как показала практика, без понимания. А нам предстоит еще закрепление в примерах, отработка навыков сравнения дробей и простых вычислений с ними, пару вечеров на это потратим, чтобы Милана увидела, что обыкновенные дроби - это легко. Общий знаменатель после них пойдёт, как по маслу.
После - десятичные, пропорции, проценты и буквенные выражения. Всё это изучали пятиклашки 85 лет назад, ибо задачник у меня за 1933 год
Конечно, я надеюсь, что появятся новые способы обучения, как в фантастических романах, с какими-нибудь кристаллами, а дети чтобы в школу ходили общаться, совершать общие дела, сразу приобщаться к труду и науке, искусству (по интересам), чтобы менять можно было направления... и на выходе становиться специалистами в любимом деле.
Учитель - это наставник и поддержка... и чтобы в нашу профессию отбирали по мастерству и душевным качествам... как и врачей...
Даже если это будет не скоро, меня успокаивают сталинские томики. Чувствую, с Березанской я и алгебру пойму, и тригонометрию, и логарифмы, чего не было в школе.
Ведь как-то Рус умудряется писать тушью и пером, после упорных боёв за свои права и свободу... Значит, и остальное осилим.
Прикрепленные файлы
-
доли 1-12.pdf (183,76К)
Количество загрузок:: 258 -
цветные доли 1-12.pdf (194,26К)
Количество загрузок:: 265
Поэтому в школьном учебнике они стоят особняком - в виде отдельного задачника. Понятно, что когда-то в СССР, после мировой, революции и гражданской войны страна из аграрной выходила в индустриальную и задачники печатали отдельно ради экономии.
Единица измерения.
День назад мы с Миланой попробовали решать дробные задания из Березанской - и не пошло: Милана на вопрос, как разделить 3 яблока на 6 человек, заявила, что по одному даст троим и принесёт еще 3.
На этой оптимистичной ноте занятие закончилось, толком не начавшись.
В старых учебниках, приступая к отработке теории практикой, сразу оперируют смешанными числами и учат выделять из дробного целое, а смешанное переводить в неправильную дробь (в современной школе - наоборот, Милана еще этого не изучала).
Оказалось, для перевода нужно еще раз разобраться, что такое неправильная дробь и дробное число в принципе.
Я даже изучила книгу "Самодельные наглядные пособия по Арифметике для V-VI классов" (автор Сахаров, 1959 г.и.). Просто находка для гуманитария, рекомендую.
Сделала файл с кругами, всяко поделёнными, распечатала 3 экз, раскрасила, заламинировала - чтобы измерять целое разными способами и раскладывать вручную целые, созданные из дробных. Вырезать до конца не успела, так что теперь, видимо, это пособие ждёт, когда до него дорастёт Рус. Файлы прикрепила к осн.посту: цветной и чб
Там, как и в "Методике" Березанской, как и в учебнике по Арифметике Киселёва, делается упор на то, что дробное число - это результат измерения, и результат этот зависит от того, что за единицу измерения взять.
И прежде, чем переходить к операциям с дробями и смешанными, мы занялись задачкой 3 и 4.
Оказалось, 2 карандаша и 1/29-ая его часть.
Наконец Милана поняла, что такое смешанное число и что знаменатель зависит от того, чем измеряем, а не что измеряем.
Рисует 1 целую, 2/3. Неправильная дробь. Как это сделать без рисунка? Принцип открыла сама. Остальные смешанные пошли без напряжения.
Позанимались очень продуктивно. Дальше - сокращение и общий знаменатель. После фундаментального копания в дробях это пойдёт проще: у Миланы быстрый ум, но ему нужно опереться на крепкое основание. И дальше "работает рука", как говорила одна наша учительница по алгебре.
Только вот в сталинских учебниках наравне с автоматизмом всегда есть задачки на смекалку и гибкость ума))) так что даже быстрым найдутся головоломки.