Сообщений в теме: 138

[magnit31]

Одна из неразрешенных до сих пор задач в мировой геометрии-это квадратура круга.
В чем суть проблемы?
Необходимо с помощью обычной линейки и циркуля начертить равный по площади круг и квадрат.И вывести формулу для любых размеров круга и квадрата.
Эта задача разрешена очень простым способом нашей соотечественницой-это моя сестра Ажаргуль Шинтекова.
Каким образом решение квадратуры круга(далее КК) застолбить за собой моей сестре?
Ведь такое не патентуется.

[shhamann]

Одна из неразрешенных до сих пор задач в мировой геометрии-это квадратура круга.
В чем суть проблемы?
Необходимо с помощью обычной линейки и циркуля начертить равный по площади круг и квадрат.И вывести формулу для любых размеров круга и квадрата.
Эта задача разрешена очень простым способом нашей соотечественницой-это моя сестра Ажаргуль Шинтекова.
Каким образом решение квадратуры круга(далее КК) застолбить за собой моей сестре?
Ведь такое не патентуется.

Вам надо с Перельманом связаться , он все объяснит...



Площадь круга вписанного в квадрат.

S = пи * (a / 2)2
Где a/2 — радиус круга, a — длина стороны квадрата.


Площадь круга описанного около квадрата.

S = пи * 0.5*a2
Где a — длина стороны квадрата.

В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.


Площадь круга

S = пи * R2
Где S — площадь круга, R — радиус круга.

Сообщение отредактировал shhamann: 17.05.2013, 01:11:33

[magnit31]

NТТтТТТТТТтттттт

Одна из неразрешенных до сих пор задач в мировой геометрии-это квадратура круга.
В чем суть проблемы?
Необходимо с помощью обычной линейки и циркуля начертить равный по площади круг и квадрат.И вывести формулу для любых размеров круга и квадрата.
Эта задача разрешена очень простым способом нашей соотечественницой-это моя сестра Ажаргуль Шинтекова.
Каким образом решение квадратуры круга(далее КК) застолбить за собой моей сестре?
Ведь такое не патентуется.

Вам надо с Перельманом связаться , он все объяснит...



Площадь круга вписанного в квадрат.

S = пи * (a / 2)2
Где a/2 — радиус круга, a — длина стороны квадрата.


Площадь круга описанного около квадрата.

S = пи * 0.5*a2
Где a — длина стороны квадрата.

В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.


Площадь круга

S = пи * R2
Где S — площадь круга, R — радиус круга.

Ты что,вопрос правильно прочитай.Эти твои школьные формулы я в 5 классе изучал.

[}{APJIu]

Каким образом решение квадратуры круга(далее КК) застолбить за собой моей сестре?

В срочном порядке напишите письмо Стинге и завку в Спортлото на выдачу патента!
Такое открытие нельзя оставить безнаказанным незамеченным!

[Рррра]

в IMU надо писать

[Lewis]

Каким образом решение квадратуры круга(далее КК) застолбить за собой моей сестре?

Пусть публикуется, скажем, в Acta Mathematica.

[magnit31]

А если здесь на сайте я опубликую решение КК,по моему это тоже будет считатся приоритетом авторства.

[Inga]

А если здесь на сайте я опубликую решение КК,по моему это тоже будет считатся приоритетом авторства.

а где гарантия, что вы не узнали это решение от соседа-гения?
вряд ли это будет чем-то считаться...
форум не научный, нашли куда выкладывать... вы бы еще соседям рассказали, надеясь, что это будет приоритетом...

идите в универ какой-нить, встречайтесь с профессорами, доказывайте, убеждайте... может вы вообще велосипед изобретаете...

[Аке]

Первым делом отправьте сами себе письмо с решением через казпочту. Дата на штемпеле ваше доказательство

ЗЫ или два, вдруг одно украдут.

Сообщение отредактировал Аке: 17.05.2013, 10:47:51

[Nebesov]

А самым первым делом вместе с сестрой прошерстите инет как следует для знакомства с уже сделанным. Начиная с википедии.
Простые решения сложных проблем приходят в голову многим людям и не всегда бывают правильными

[dlad]

квадратура круга.

Что это?

[2774259]

Из википедьки:


Математическое доказательство невозможности квадратуры круга не мешало многим энтузиастам тратить годы на решение этой проблемы. Тщетность исследований по решению задачи квадратуры круга перенесла этот оборот во многие другие области, где он попросту обозначает безнадежное, бессмысленное или тщетное предприятие. См. также Вечный двигатель.


Если принять за единицу измерения радиус круга и обозначить x длину стороны искомого квадрата, то задача сводится к решению уравнения: 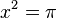, откуда: 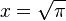. Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины . Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа , которая была доказана в 1882 годуЛиндеманом.
Однако эту неразрешимость следует понимать, как неразрешимость при использовании только циркуля и линейки. Задача о квадратуре круга становится разрешимой, если, кроме циркуля и линейки, использовать другие средства (например,квадратрису). Простейший механический способ предложил Леонардо да Винчи. Изготовим круговой цилиндр с радиусом основания и высотой , намажем его чернилами и прокатим по плоскости. За один полный оборот цилиндр отпечатает на плоскости прямоугольник площадью 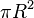. Располагая таким прямоугольником, уже несложно построить равновеликий ему квадрат.

[magnit31]

Когда я помещю здесь пояснения решения КК(очень простое)-вы все 100% согласитесь ,что задача решена.Только с помощью линейки и циркуля каждый убедится проверив мои доводы-сам начертит круг и квадрат равные по площади.Легко.

квадратура круга.

Что это?

Сообщение отредактировал magnit31: 17.05.2013, 12:20:36

[unikym]

атвичаю! квадратура (квартирная) - Круга..
доказал?

[Очень Важная Персона]

Аффтар, зачем Вам с мелочевкой, типо квадратуры какой-то, возиться? Давайте сразу на пертетуум мобиле замахнитесь, ящитаю!

[ЙОЛКО]

Только с помощью линейки и циркуля каждый убедится проверив мои доводы-сам начертит круг и квадрат равные по площади.Легко.

а я то сижу и думаю, чем бы мне на работе заняться, ага

[magnit31]

Аффтар, зачем Вам с мелочевкой, типо квадратуры какой-то, возиться? Давайте сразу на пертетуум мобиле замахнитесь, ящитаю!

Отсталый вы человек-очень неважная персона.Перпеттум мобиле мною уже изобретен.

[gis]

давайте сюда решение, вгоните в краску местных физиков и математиков, а может и в анналы ВВ попадете

[magnit31]

А если здесь на сайте я опубликую решение КК,по моему это тоже будет считатся приоритетом авторства.

а где гарантия, что вы не узнали это решение от соседа-гения?
вряд ли это будет чем-то считаться...
форум не научный, нашли куда выкладывать... вы бы еще соседям рассказали, надеясь, что это будет приоритетом...

идите в универ какой-нить, встречайтесь с профессорами, доказывайте, убеждайте... может вы вообще велосипед изобретаете...

Живу в степи,в радиусе 100 км соседей нет.А если ты считаешь что у кого то я украл,пусть тот скажет об этом.Язык наверное у него есть.Ну это обычная зависть.

[magnit31]

давайте сюда решение, вгоните в краску местных физиков и математиков, а может и в анналы ВВ попадете

Для решения задачи о квадратуре круга надо по горизонтальному радиусу отложить отрезок 63,6, (катет) от него вверх 77,2(катет), соединить центр круга с концом второго вертикального катета. Полученный центральный угол равен 50 градусам и 36 минутам (50,56 градусов). Сторона квадрата будет равна а=R+R*sin50,57. Так как по условию задачи должно выполняться равенство а=R*корень из ПИ, то есть а=R+R*0.772. А любое число от 0 до 1 можно представить как синус какого-либо угла с достаточной точностью.